Numerische Simulationen, Teil 2
Wärmeleitfähigkeit von Hochlochziegeln: Grundlagen – Messtechnik – Simulation

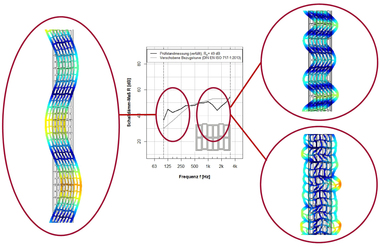
In der Ausgabe 1-2021 der ZI Ziegelindustrie International wurde bereits ein Artikel von M.Sc. Darya Ivanova vom Institut für Ziegelforschung Essen e.V. über den „Einsatz numerischer Simulationen zur Untersuchung und Verbesserung des akustischen Verhaltens von Hochlochziegeln“ veröffentlicht. In diesem Artikel soll es nun um die bauphysikalische Eigenschaft der Wärmeleitfähigkeit und die numerischen und messtechnischen Möglichkeiten der Bestimmung gehen.

1 Grundlagen zur Wärmeleitfähigkeit

Bei der Wärmeleitfähigkeit handelt es sich um eine temperaturabhängige, materialspezifische Größe eines reinen Festkörpers, einer reinen Flüssigkeit oder eines reinen Gases, die den Wärmestrom in Joule angibt, der pro Sekunde durch eine 1 m² große und 1 m dicke Schicht eines bestimmten Stoffes hindurchgeht. Das übliche Formelzeichen ist der kleine griechische Buchstabe λ (Lambda) mit der Einheit J/(m·s·K) bzw. W/(m·K). Wird bei Baustoffen von der Wärmeleitfähigkeit gesprochen, handelt es sich streng genommen um eine Mischform unterschiedlicher Wärmeübertragungsmechanismen. Insbesondere Dämmstoffe, aber auch mineralische Baustoffe wie Ziegelscherben oder organische Baustoffe wie Holz haben ein mehr oder weniger komplexes Porengefüge. Bei derartigen Baustoffen tritt neben der Wärmeleitung über das reine Festkörpergerüst, die Gasphase sowie Flüssigwasser in den Poren, auch Wärmestrahlung zwischen den Oberflächen der Poren und Konvektion über die Luft in den Poren auf. Bei Baustoffen mit mittlerer bis hoher Dichte, wie z.B. Ziegelscherben, sind die Anteile von Strahlung und Konvektion über das Porengefüge zu vernachlässigen. Maßgeblich an der Wärmeübertragung in einem Ziegelscherben sind die Wärmeleitung über das Festkörpergerüst sowie der Porenluft.

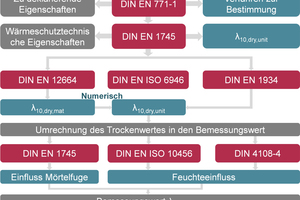
Aus diesen Gründen ist es üblich und durchaus sinnvoll, bei diesen Baustoffen allgemein von der Wärmeleitfähigkeit als Materialeigenschaft zu sprechen. Betrachtet man jedoch einen Hochlochziegel mit seiner komplexen Steggeometrie sowie der möglichen Dämmstofffüllung der Lochkammern, sollte allgemein von der resultierenden Wärmeleitfähigkeit gesprochen werden, um sich von der reinen Materialwärmeleitfähigkeit zu unterscheiden. Zur Abgrenzung der unterschiedlichen Wärmeleitfähigkeiten von Ziegelscherben, Hochlochziegel und HLZ-Mauerwerk inklusive Mörtelfugen liefert die DIN EN 1745:2012 [2] entsprechende Kennzeichnungen über die Indizes, deren Vielfalt zunächst überfrachtet wirken mag, jedoch eine unmissverständliche Kommunikation ermöglicht. Grundsätzlich wird zwischen den Trockenwerten und den Bemessungswerten der Wärmeleitfähigkeit unterschieden, welche durch Indizes spezifiziert werden.

Hierbei handelt es sich um die relevantesten Formelzeichen und Indizes, die in den entsprechenden Normen verwendet werden. »Abb. 2 soll die normativen Verweise und Abhängigkeiten untereinander etwas verdeutlichen. Zu deklarierende Eigenschaften von Mauerziegeln sowie die Verfahren zu deren Bestimmung sind in DIN EN 771-1 [3] festgelegt. Zur Ermittlung der wärmeschutztechnischen Eigenschaften wie der Wärmeleitfähigkeit wird auf die DIN EN 1745 verwiesen, in der wiederum spezifiziert wird, mit welchen Verfahren und Methoden die Wärmeleitfähigkeit bestimmt werden kann. Neben der direkten Messung des Wärmedurchgangs durch einen Wandprüfkörper im Heizkastenverfahren nach DIN EN 1934 [4], welches den λ_10,dry,mas-Wert liefert, wird auf die DIN EN ISO 6946 [5] verwiesen, in der die Wärmeübergangsbedingungen sowie die Berechnung des Wärmedurchgangswiderstandes R und des Wärmedurchgangskoeffizienten U beschrieben sind. Über die Bestimmung der Scherbenwärmeleitfähigkeit λ_10,dry,mat im Plattengerät nach DIN EN 12664 [6], lässt sich mittels numerischer Methoden gemäß DIN EN ISO 10211 [7] die resultierende Wärmeleitfähigkeit des gesamten Hochlochziegels berechnen. Unter Berücksichtigung des Mörtelfugeneinflusses, beschrieben in DIN EN 1745 sowie des Feuchteeinflusses nach DIN EN ISO 10456 bzw. DIN 4108-4 [8], lässt sich der Bemessungswert berechnen (»Abb. 2). Der Bemessungswert der Wärmeleitfähigkeit eines Baustoffes ist maßgebend, wenn es darum geht, ein Außenbauteil eines Gebäudes hinsichtlich seiner energetischen Qualität bzw. seiner wärmedämmenden Wirkung zu beurteilen und letztendlich den Heizwärmebedarf des gesamten Gebäudes zu berechnen.

Wie der Bemessungswert aus dem Messwert ermittelt wird, soll nachfolgend anhand »Abb. 3 erläutert werden. Aus der anliegenden Spannung U und der Stromstärke I berechnet sich der Wärmestrom Q, aus dem sich wiederum über die Berücksichtigung der Probekörperfläche und –dicke sowie der Temperaturdifferenz die Scherbenwärmeleitfähigkeit λ_10,dry,mat berechnen lässt. Abweichungen zum oberen Grenzwert der Netto-Trockenrohdichte sind über den Extrapolationsfaktor zu berücksichtigen und entsprechend zu korrigieren. Durch die Multiplikation mit dem Feuchtekorrekturfaktor Fm nach DIN 4108-4 für Ziegel, wird der Ausgleichsfeuchteeinfluss bei 80 % rel. Luftfeuchte und 23 °C auf die Wärmeleitfähigkeit berücksichtigt. Mit den Bemessungswerten der Wärmeleitfähigkeit für den Ziegelscherben und einer eventuellen Dämmstofffüllung wird die Wärmestromdichte entsprechend des geometrischen Hochlochziegelmodells in 2D mittels FEM-Software berechnet. Über Wärmestromdichte, Dicke des Ziegels und Temperaturdifferenz zwischen den Oberflächen der warmen und kalten Seite, wird der Bemessungswert des Ziegels λ_design,unit(,100 %) berechnet. Da es sich um ein 2D-Modell handelt, wird der Mörtelfugeneinfluss vereinfacht flächenanteilig berücksichtigt. Ausgehend von einer Mörtelfugendicke von 1 mm und einer Ziegelhöhe von 249 mm, ergeben sich Flächenanteile von 0,4 bzw. 99,6 %. Der Bemessungswert für das Ziegelmauerwerk berechnet sich entsprechend Abbildung 3 unter Berücksichtigung des Feuchtekorrekturfaktors von Mörtel entsprechend DIN 4108-4.

2 Messtechnische Bestimmung der

Scherbenwärmeleitfähigkeit

Die maßgebende Eingangsgröße zur numerischen Bestimmung des Wärmestroms Q durch einen Hochlochziegel und der daraus abzuleitenden resultierenden Wärmeleitfähigkeit λ_10,dry,unit oder λ_10,dry,mas ist die gemessene Scherbenwärmeleitfähigkeit λ_10,dry,mat und ggf. die Wärmeleitfähigkeit einer Dämmstofffüllung. Da sowohl die Messung als auch die anschließende Simulation unter stationären Randbedingungen stattfinden, ist eine Berücksichtigung der Scherbenrohdichte und spezifischen Wärmekapazität nicht erforderlich, dennoch kann die gemessene Scherbenrohdichte bei der Bewertung der Ergebnisse hilfreich sein. Die Messung der Scherbenwärmeleitfähigkeit am Institut für Ziegelforschung Essen e.V. erfolgt über ein neues Einplattengerät gemäß DIN EN 12664:2001 sowie zusätzlich zur Kontrolle über den ISOMET-Schnelltest. Eventuell erforderliche Messungen der Wärmeleitfähigkeit einer Dämmstofffüllung erfolgen im gleichen Gerät, jedoch nach DIN EN 12667. Beim Einplattengerät handelt es sich um ein Messgerät, mit dem der Wärmestrom durch einen Probekörper gemessen wird. Für die Messung des Wärmestroms durch den Probekörper müssen horizontale Wärmeströme in der Ebene des Probekörpers sowie der Heizplatte minimal gehalten werden. Hierfür wird die Probe in eine Probeaufnahme aus einem wärmedämmenden Flies eingebettet (»Abb. 4).

Zuvor wird die Probe aus einem Außensteg des entsprechenden Hochlochziegels herausgeschnitten, planparallel geschliffen und auf die Abmessungen der Messfläche zugeschnitten. Anschließend wird der vorbereitete Prüfkörper bei 105 °C bis zur Massekonstanz getrocknet und danach im Exsikkator abgekühlt, um eine Feuchteaufnahme aus der Umgebung zu unterbinden. Danach wird der Probekörper im Einplattengerät eingebaut. Zwischen der Heiz- und Kühlplatte wird ein definiertes Temperaturgefälle eingestellt, woraus sich der Wärmestrom durch den Probekörper ergibt. Der Wärmestrom wird aus der Leistung, die der Heizplatte zugeführt werden muss. berechnet. Die Messung erfolgt unter stationären Randbedingungen. Aus dem konstanten Wärmestrom Q (Heizleistung) im stationären Zustand, der Dicke d und Fläche A des Probekörpers sowie der Temperaturdifferenz wird die Wärmeleitfähigkeit der darrtrockenen Materialprobe nach Gleichung 1 (»Abb. 3) in einem Intervall von 30 Sekunden berechnet.

3 Numerische Bestimmung der resultierenden

Wärmeleitfähigkeit

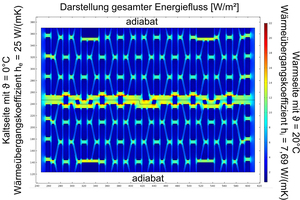
Für die numerische Bestimmung der resultierenden Wärmeleitfähigkeit von Hochlochziegeln gibt die DIN EN 1745 vor, dass die FEM-Software die Randbedingungen und Vorgaben der DIN EN 10211 erfüllen muss. Hierbei handelt es sich um die Norm zur Beschreibung der Wärmebrücken im Hochbau mittels detaillierter Berechnungen. Alle gängigen Wärmebrückenprogramme, die nach DIN EN ISO 10211 validiert sind, eignen sich demnach auch für die Berechnung der resultierenden Wärmeleitfähigkeit von Hochlochziegeln, da hier nichts anderes, als Wärmeströme und Oberflächentemperaturen berechnet werden. All diesen Programmen gemein ist jedoch der vereinfachte Ansatz der Berücksichtigung der Wärmeübertragung durch Strahlung und Konvektion nach DIN EN ISO 6946, bei dem für luftgefüllte Kammern äquivalente Wärmeleitfähigkeiten eingesetzt werden. Da im Rahmen der Forschung oftmals auch die Notwendigkeit besteht, die Wärmeübertragungsmechanismen separat zu betrachten, wurde auf ein Modell in der FEM Software Comsol Multiphysics zurückgegriffen und dort die Wärmeleitung mit der Wärmestrahlung gekoppelt. Das Modell wurde dann auf die Anforderungen der DIN EN 1745 und DIN EN ISO 10211 angepasst und validiert. Die Wärmeübertragung mittels Konvektion innerhalb der luftgefüllten Lochkammern kann in den meisten Fällen vernachlässigt werden, da große Kammern mit Dämmstoff gefüllt sind und filigrane Lochbilder so kleine Kammern aufweisen, in denen Konvektion vernachlässigbar ist [9] [10] [11]. Abbildung 4 zeigt zur Beschreibung des numerischen Modells das Ergebnis einer Berechnung des Energieflusses.

Nach Vorgabe der DIN EN 1745 wird der Hochlochziegel in der Symmetrieachse in Dickenrichtung getrennt und im Bereich der Stoßfuge wieder zusammengesetzt. So soll berücksichtigt werden, dass im Bereich der Stoßfuge ein erhöhter Energiefluss stattfindet. Die Wärmeübergangskoeffizienten für innen und außen werden von der DIN EN ISO 6946 vorgegeben. Sie beschreiben in diesem Fall den Übergang einer Wärmemenge an der Grenzfläche von der Raumluft auf die Wandoberfläche und von der Außenoberfläche an die Außenluft. Vereinfachend wird im Bauwesen von Konstanten ausgegangen, die sich aus dem konvektiven Wärmeübergang, der maßgeblich durch die Strömungsgeschwindigkeit der vorbeistreichenden Luft bestimmt wird und dem Wärmeübergang infolge Strahlung, der sich maßgeblich aus dem thermischen Emissionsgrad in Verbindung mit dem Stefan-Boltzmann-Gesetz berechnen lässt. Aus den Berechnungen folgen auf Basis der Temperaturrandbedingungen, einer Windgeschwindigkeit von 4 m/s außen sowie einem typischen Emissionsgrad für mineralische Baustoffe von 0,9 die in »Abb. 4 aufgeführten Wärmeübergangskoeffizienten. Anstelle der Temperaturrandbedingungen mit 20 °C innen und 0 °C außen würden in der numerischen Berechnung natürlich auch 1 °C innen und 0 °C außen zu den gleichen Ergebnissen führen, da zwischen Wärmestromdichte und Temperaturdifferenz ein linearer Zusammenhang besteht und sich die Wärmeleitfähigkeit immer auf ein 1 K Temperaturdifferenz bezieht. Die Temperaturdifferenz von 20 K ist aus den Messungen übernommen worden, um die ermittelten Oberflächentemperaturen und Wärmeströme besser vergleichen zu können. Somit sind nun die äußeren Randbedingungen des Modells beschrieben.

Für die Berechnungen müssen jedoch noch die Materialparameter und die Strahlungsrandbedingungen zugewiesen werden. Der gesamten Stegfläche wird die gemessene Scherbenwärmeleitfähigkeit zugewiesen. Sollte diese noch nicht ermittelt werden können, da es sich um eine mögliche steggeometrische Optimierung handelt und das Material noch nicht endgültig steht, lässt sich durch die Simulation mit zwei unterschiedlichen Scherbenwärmeleitfähigkeiten der lineare Zusammenhang zur resultierenden Wärmeleitfähigkeit des gesamten Hochlochziegels grafisch darstellen oder über die entsprechende Geradengleichung berechnen. So lässt sich vorab näherungsweise abschätzen, welche Scherbenwärmeleitfähigkeit bei der entsprechend untersuchten Geometrie erforderlich ist, um eine gewünschte resultierende Wärmeleitfähigkeit des Mauerwerks zu erreichen. Sinnvoll ist hier vor allem der Relativvergleich zwischen einer bekannten Geometrie und Varianten im Rahmen der Produktoptimierung.

Sind die Lochkammern mit Dämmstoff gefüllt, muss diesen ebenfalls eine entsprechende Materialwärmeleitfähigkeit zugewiesen werden. Dann handelt es sich lediglich um Wärmetransport in Feststoffen, der sich auf die Wärmeleitung beschränkt. Handelt es sich um ungefüllte Luftkammern liegt eine Fluid-Struktur-Kopplung vor, bei der für das Fluid (Luft) zusätzlich zur temperaturabhängigen Wärmeleitfähigkeit noch die Strahlungsrandbedingungen festgelegt werden müssen. Hierfür werden allen inneren Oberflächen, die im gegenseitigen Strahlungswärmeaustausch stehen, der Emissionsgrad ε sowie die strahlungsphysikalischen Randbedingungen, die für die Oberflächen gelten sollen, zugewiesen. Dies erfolgt über sogenannte diffus-spektrale Oberflächen, für die auf Basis des Stefan-Boltzmann-Gesetzes entsprechend der Oberflächentemperatur und des Emissionsgrades die Strahlungsbilanz für jeden Knoten auf einer Oberfläche berechnet wird. Somit sind alle erforderlichen Eingangsparameter zur numerisch gestützten Berechnung der resultierenden Wärmeleitfähigkeit von Hochlochziegeln beschrieben und definiert.

4 Anwendungsbeispiele

Ein kleiner Vergleich in »Tabelle 2 zeigt die Ergebnisse von Wandmessungen im Prüfstand nach DIN EN 1934 sowie numerischer Simulationen und anschließender Berechnung des Bemessungswertes für Mauerwerk.

Die Abweichung zwischen Messung und Numerik liegt zwischen -1,5 und -6 % bezogen auf das Messergebnis. Die Abweichungen entstehen aufgrund vieler Faktoren. Der größte Unterschied besteht im Hinblick auf die konstanten, idealen Randbedingen und Materialparameter, ohne natürliche Schwankungen. Hier besteht einerseits ein Vorteil der Simulation, da die Ergebnisse vollständig und dauerhaft reproduzierbar sind und so der Relativvergleich unterschiedlicher Varianten unmittelbar auf die Parameter- oder Geometrievariationen bezogen werden kann. Dies ist bei Messungen kaum möglich, da keine konstanten Randbedingen vorliegen. Andererseits führen eben die idealen Randbedingungen und Vereinfachungen wie die zweidimensionale Betrachtung und isotrope Materialeigenschaften zu völlig plausiblen Abweichungen, die bei der Bewertung berücksichtigt werden müssen. Dennoch reicht die Berechnung unter diesen Randbedingungen für eine Abschätzung des zu erwartenden Messergebnisses mit ausreichender Genauigkeit aus, vor allem wenn auch noch Referenzwerte vorliegen.

In der nachfolgenden »Tabelle 3 sind anhand leicht abstrahierter Geometrien einmal ansatzweise die Möglichkeiten der Relativvergleiche aufgezeigt. Geometrischen Variationen sind hier keine Grenzen gesetzt, egal ob Rundungen, Bögen, Diagonalen, Löcher, alles lässt sich mit numerischen Methoden berücksichtigen und hinsichtlich der Auswirkungen auf die resultierende Wärmeleitfähigkeit bewerten. So lässt sich eine Aussage treffen, ob eine Variation am Produkt tendenziell eine Verbesserung oder eine Verschlechterung bewirkt. Vor allem der parallele Vergleich der Auswirkungen auf die Schalltransmission und die Wärmeleitfähigkeit sind hier besonders wichtig. Bei den dargestellten Inhalten handelt es sich um abstrahierte Geometrien, die lediglich die Möglichkeiten und das Grundprinzip aufzeigen sollen wie Relativvergleiche durchgeführt werden können.

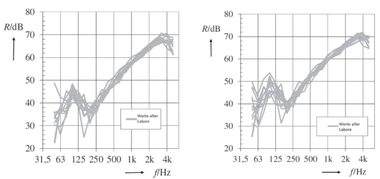
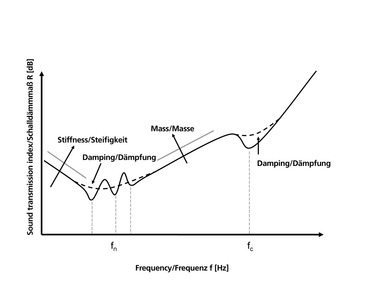
Einiges von den Ergebnissen ist sicher zumindest qualitativ bekannt, wie zum Beispiel die Verbesserung der resultierenden Wärmeleitfähigkeit durch versetzte Stege in Wanddickenrichtung. Interessant wird es, wenn die Unterschiede zwischen einem Mittelsteg und zwei dünneren Mittelstegen gleicher Gesamtdicke sowohl hinsichtlich der Wärmeleitfähigkeit als auch der Schalltransmission betrachtet wird. Der Unterschied in der Wärmeleitfähigkeit ist mit 0,7 % sehr gering, bei der Betrachtung des frequenzabhängigen Schalldämm-Maßes wird sich jedoch herausstellen, dass gerade in den hohen Frequenzen ab 1000 Hz eine deutliche Verbesserung auftritt, da der Einbruch im Bereich der Dickenschwingungen aufgrund der höheren Steifigkeit der Geometrie viel geringer ausfällt und hin zu höheren Frequenzen verschoben wird. Das ist jetzt noch keine pauschal gültige Aussage und der Einzelfall ist detailliert zu untersuchen, jedoch werden derartige steggeometrische und materialspezifische Zusammenhänge in einem aktuellen Forschungsprojekt systematisch untersucht.

5 Möglichkeiten und Grenzen

Grundsätzlich gilt, dass die Ergebnisse die eine Messung oder auch eine Berechnung, egal ob analytisch oder numerisch gelöst, hervorbringt, kritisch zu hinterfragen und auf Plausibilität zu prüfen sind. Fehlerquellen gibt es auf beiden Seiten. Messungen in Prüfständen unterliegen immer dem Einfluss äußerer Randbedingungen, welcher sich zwar minimieren aber nicht ausschließen lässt. Der Faktor Mensch kann sowohl bei Messungen als auch Berechnungen als Fehlerquelle auftreten, was sich durch eine entsprechende Qualifikation aber ebenfalls minimieren lässt. Messungen in Prüfständen, egal ob es um das Schalldämm-Maß oder den Wärmedurchgang geht, sind notwendig und im Rahmen der Erwirkung allgemein bauaufsichtlicher Zulassungen auch gefordert. Die numerische Bestimmung der Schalltransmission und des Wärmedurchgangs durch Hochlochziegel sollte jedoch das Mittel der Wahl in den frühen Phasen der Produktentwicklung sein, bevor überhaupt ein Mundstück produziert wird.

Zu diesem Zeitpunkt steht mit den numerischen Methoden eine außerordentlich effiziente Möglichkeit zur Bewertung der zu erwartenden Schalldämmung und Wärmeleitfähigkeit zur Verfügung. In dieser frühen Phase einer Produktentwicklung oder -optimierung bietet die Simulation die einzige Möglichkeit einen Relativvergleich der zu untersuchenden Produkteigenschaft durchzuführen, der sich ausschließlich auf die Geometrie- oder Materialparameter des Produktes beschränkt, da die Randbedingungen ideal und konstant sind. Zudem ergeben sich große Einsparungen bei den Aufwendungen für Material, Zeit, Produktions- und Energiekosten. Die Modelle funktionieren so gut, dass innerhalb eines Relativvergleichs belastbare Aussagen möglich sind. Darüber hinaus lässt sich im Rahmen einer ganzheitlichen Betrachtung des zu untersuchenden Produktes eine Abschätzung mit ausreichender Genauigkeit über die zu erwartenden Produkteigenschaften treffen. Für eine derartige Aussage müssen jedoch auch die Grenzen der angewandten numerischen Methoden bekannt sein.

Erfolgt eine Beauftragung zur numerischen Bestimmung des Wärmedurchgangs durch Hochlochziegel auf Basis einer vorhandenen Lochgeometrie sowie der gemessenen Scherbenwärmeleitfähigkeit, muss von Anfang an klar sein, dass das numerische Ergebnis nicht exakt dem zu erwartenden Ergebnis einer Wandmessung im Heizkasten entsprechen kann. Die Gründe hierfür sind vielfältig, maßgeblich sind aber die idealen Randbedingungen, die konstanten Materialparameter und die Vereinfachung durch die Betrachtung einer zweidimensionalen Geometrie im numerischen Modell. Aus diesen Gründen weisen die numerisch bestimmten, resultierenden Wärmeleitfähigkeiten etwa 1,5 bis 6 % geringere Werte im Vergleich zur Wandmessung auf. Dies muss bei der Bewertung der absoluten Ergebnisse dringend beachtet und kommuniziert werden. Für einen Relativvergleich eignen sich die numerischen Methoden sehr gut und deutlich besser als Messungen, da der Einfluss der Randbedingungen und Materialabweichungen ausgeklammert wird und sich der Vergleich unmittelbar auf Materialparameter- oder Geometrieänderungen bezieht. Erst wenn nach den numerischen Untersuchungen eine Variante für geeignet befunden wird, sollten geringe Mengen produziert und messtechnisch untersucht werden.

6 Zusammenfassung

Numerische Methoden können und sollten in frühen Stadien der Produktentwicklung oder Produktoptimierung aufwendige und teure Messungen ersetzen, wenn es darum geht, eine Entwicklung durch Relativvergleiche der relevanten Eigenschaften wie z.B. der Wärmeleitfähigkeit zu bewerten. Diese Methoden eignen sich hierfür in vielen Fällen besser, da Ergebnisse reproduzierbar und äußere Einflüsse ausgeschlossen sind sowie eine unmittelbare Bewertung sowie isolierte Betrachtung der Optimierungen möglich ist. Auch zur Abschätzung der zu erwartenden Messwerte sind derartige Methoden geeignet, hier müssen die Ergebnisse jedoch im Hinblick auf die Grenzen der numerischen Modelle bewertet und auch entsprechend kommuniziert werden. So stellen sie eine effiziente und nachhaltige, weil ressourcenschonende Möglichkeit der Untersuchung von Produkteigenschaften dar.