Messtechnische und numerische Analysen des akustischen Verhaltens von einzelnen Hochlochziegeln

1 Einleitung

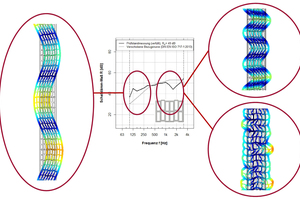
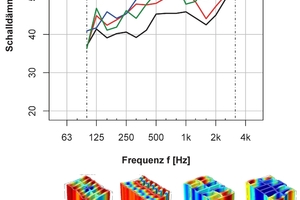
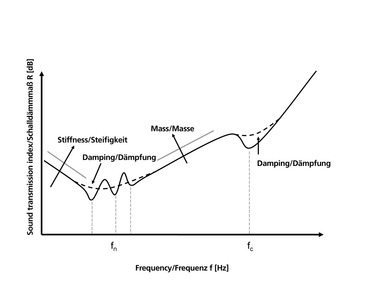
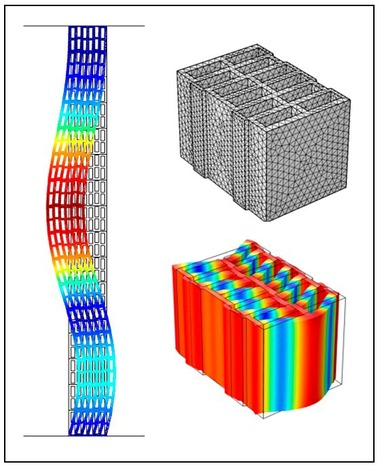
Die Geometrie der Lochung der Hochlochziegel beeinflusst, wie auch die Rohdichte, das Schalldämm-Maß der gesamten Wand. Körperschallmessungen wurden bereits von Gösele [1, 2] und dem Fraunhofer-Institut für Bauphysik [3, 4, 5] durchgeführt, die Dickenresonanzen bzw. Dickenschwingungen der einzelnen Hochlochziegel feststellten. Bei Dickenschwingungen bewegen sich die gegenüberliegenden Oberflächen der Hochlochziegel im Gegensatz zu den Biegeschwingungen gegenphasig. »1 veranschaulicht das frequenzabhängige Schwingverhalten einer Wand aus Hochlochziegeln. Im tiefen bis mittleren Frequenzbereich bis ca. 500 Hz schwingt die Wand nahezu wie ein einschaliges, homogenes Bauteil. Ab ca. 500 Hz treten sowohl Biege- als auch Dickenschwingungen auf. In »1 sind sowohl Dickenschwingungen mit gegenphasig schwingenden als auch die Biegeschwingungen mit gleichphasig schwingenden Oberflächen zu erkennen.

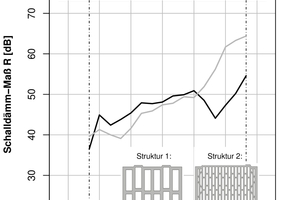
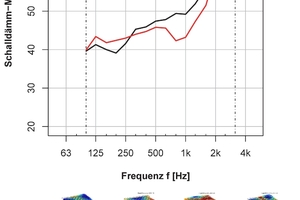
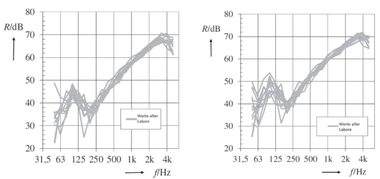
Dickenschwingungen treten sowohl in homogenen als auch in inhomogenen Bauteilen auf. Jedoch treten die Dickenschwingungen bei homogenen Bauteilen im Gegensatz zu inhomogenen Hochlochziegelwänden weit oberhalb des bauakustisch relevanten Frequenzbereichs auf. Untersuchungen von Koch und Maysenhölder [3, 4, 5] zeigen, dass bei Dickenschwingungen nicht die Oberflächen der gesamten Wand, sondern die Oberflächen des Steins gegeneinander schwingen. Dabei wurden deutlich geringere Schwingungen in den Fugen zwischen den Steinen im Vergleich zur Mitte der Steinoberfläche, wie in »1 zu erkennen, beobachtet. Maysenhölder untersuchte das Schwingverhalten von Lochsteinen mithilfe der experimentellen Modalanalyse und stellte so den Zusammenhang zwischen den Dicken- und Biegeschwingungen der Lochsteine sowie der Änderung der Schalldämmung der gesamten Wand auf. In welchem Frequenzbereich und wie stark die Änderung in der Schalldämmung ist, wird durch die Geometrie der Lochung, von der Größe des Ziegels und von den Materialeigenschaften des Scherbens beeinflusst. In »2 sind zwei Prüfstandsmessungen von einem fein- und einem großgelochten Hochlochziegel dargestellt.

In diesem Beispiel ist zu erkennen, wie unterschiedlich der Verlauf der Schalldämmung der beiden Hochlochziegel im Bereich zwischen 500 und 2 000 Hz ist. Der großgelochte Hochlochziegel weist gegenüber dem feingelochten Ziegel eine veränderte Schalldämmung bei ca. 1 600 Hz auf. Dabei ist bei dem feingelochten Ziegel keine stark ausgeprägte Änderung in der Schalldämmung zu erkennen. Dagegen steigt das Schalldämm-Maß, ab ca. 500 Hz, nicht wie erwartet nach dem Bergerschen Massengesetz um 6dB/Oktave an, sondern hat einen viel flacheren Verlauf zwischen 500 und 1 000 Hz. Diese Änderungen in der Schalldämmung sind auf die Dicken- und Biegeschwingungen der einzelnen Hochlochziegel zurückzuführen. Schon aus dem Verlauf des Schalldämm-Maßes kann beobachtet werden, dass sich die Einzelsteinschwingungen von Hochlochziegel zu Hochlochziegel unterscheiden.

2 Experimentelle und numerische Modalanalyse

Eine in der akustischen Messtechnik weit verbreitete Untersuchungsform zur Analyse des dynamischen Verhaltens von schwingungsfähigen Systemen, die dynamischen Beanspruchungen ausgesetzt sind, ist die sogenannte Modalanalyse. Mithilfe der Modalanalyse können die für ein System charakteristischen Modalfrequenzen mit den dazugehörigen Modenformen sowie modalen Dämpfungen bestimmt werden (auch Eigenfrequenzen, Eigenschwingungen sowie Eigendämpfungen genannt). Stimmt eine Erregerfrequenz mit einer Eigenfrequenz eines Systems überein, kommt es zu einer resonanzartigen Amplitudenerhöhung, woraus je nach System negative Auswirkungen, wie Instabilitäten, Versagen oder Fehlfunktionen, resultieren können. In der in diesem Artikel thematisierten Bauakustik führt eine resonanzartige Amplitudenerhöhung zu einer erhöhten Schalltransmission und somit zu einer erhöhten Schallabstrahlung eines Bauteils. Eine Modalanalyse ist nur für lineare Modelle definiert und liefert keinerlei Aussagen über die tatsächlich im Modell auftretenden Spannungen sowie Verschiebungen unter einwirkenden Lasten.

Innerhalb der experimentellen Modalanalyse wird die zu untersuchende Struktur an definierten Punkten angeregt. Dafür kann beispielsweise ein Impulshammer (impulsartige Anregung) oder ein Shaker (Signalanregung) verwendet werden. Die daraus resultierenden Systemantworten (Beschleunigung, Schnelle oder Auslenkung) werden wiederum an definierten Messpunkten ermittelt. Aus den so bekannten Systemanregungen sowie den dazugehörigen Systemantworten ergeben sich sogenannte Übertragungsfunktionen, die das Schwingverhalten der Struktur beschreiben und aus denen sich weiter die modalen Parameter bestimmen lassen. Hierbei sind die Ergebnisse insbesondere von den vorherrschenden Randbedingungen abhängig. Zudem sind bei der experimentellen Modalanalyse die Anzahl sowie Platzierung der Messpunkte (Diskretisierung) von Bedeutung, um aussagekräftige Ergebnisse zu erhalten. Dabei müssen alle definierten Messpunkte der zu untersuchenden Struktur zugänglich sein.

Neben der experimentellen Modalanalyse kann die Eigenwertanalyse für eine Bestimmung der modalen Parameter (Eigenfrequenz, Eigenschwingung, Eigendämpfung) eines schwingungsfähigen Systems auch analytisch durchgeführt werden. Dafür werden die zu analysierenden Systeme in Ersatzsysteme, bestehend aus Massen, Federn sowie Dämpfern, überführt und deren Bewegungsgleichungen in der Form

⇥(1)

als System aus gekoppelten Differenzialgleichungen formuliert. Hierbei beschreiben

M die Massenmatrix

D die Dämpfungsmatrix

K die Steifigkeitsmatrix

den Beschleunigungsvektor

den Geschwindigkeitsvektor

den Verschiebungsvektor

den Kraftvektor der systemanregenden Kräfte

Werden harmonische ungedämpfte Schwingungen analysiert, ergibt sich das System zu

⇥(2)

Durch einen Lösungsansatz für eine harmonische Schwingung ergibt sich ein Eigenwertproblem, das nach Diskretisierung und einer numerischen Lösung die gewünschten Eigenwerte liefert. Man spricht von einer linearen Modalanalyse. Mithilfe der numerischen Modalanalyse können unkompliziert größere Frequenzbereiche analysiert werden.

Ein Vorteil der numerischen Modalanalyse ist deren bereits in einem sehr frühen Planungsstadium mögliche Anwendung, lange bevor eine praktische Umsetzung erfolgt. Ebenso können durch den Einsatz einer numerischen Modalanalyse komplizierte Geometrien sowie größere Frequenzbereiche schnell und kostengünstig analysiert werden. Da jedoch bei der Modellerstellung für eine numerische Modalanalyse immer einige Vereinfachungen sowie Annahmen (u. a. Materialeigenschaften und Randbedingungen) getroffen werden müssen, sind eine parallele Anwendung von experimenteller und numerischer Modalanalyse sowie ein Vergleich der Ergebnisse zur Validierung sinnvoll [6, 7, 8].

3 Vergleich zwischen experimenteller und numerischer Modalanalyse

Für die experimentellen und numerischen Untersuchungen wurden ein fein- und ein großgelochter Hochlochziegel, wie in »2 dargestellt, verwendet.

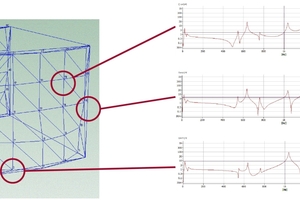
Dabei wurden die Stirnoberflächen der Hochlochziegel mit einem Messraster versehen und diese mit einem Impedanzhammer angeregt. Zudem wurde ein Beschleunigungsaufnehmer auf der Stirnseitenoberfläche des Hochlochziegels befestigt. Bei Untersuchungen einzelner Hochlochziegel wurden die Ziegel auf einer Luftpolsterfolie positioniert, um den Untergrund von dem zu messenden Hochlochziegel zu entkoppeln. Dabei ist es wichtig, dass aufgrund des dadurch entstandenen Masse-Feder-Systems die Resonanzfrequenz möglichst tief und außerhalb des zu messenden Frequenzbereichs liegt. Nach Anregung des Hochlochziegels mit dem Impedanzhammer an den jeweiligen Messpunkten erhält man die jeweilige Übertragungsfunktion zwischen Anregungspunkt und Aufnahmepunkt, an dem der Beschleunigungsaufnehmer befestigt ist. In »3 sind die gemessenen Übertragungsfunktionen mit der experimentellen Modalanalyse dargestellt.

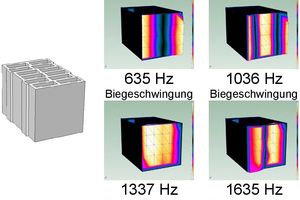
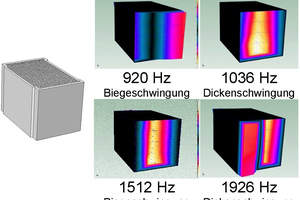
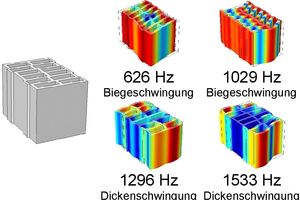
Die starken Spitzen weisen auf die zuvor beschriebenen Eigenschwingungen hin. Bei dieser Untersuchung war es notwendig, beide Stirnseiten des Hochlochziegels mittels Modalanalyse zu untersuchen, damit anschließend aus dem in »3 dargestellten Hochlochziegelmodell die Art der Schwingung identifiziert werden kann. Bei gleichphasiger Schwingung der beiden Oberflächen kann die Eigenfrequenz einer Biegeschwingung und bei einem gegenphasigen Schwingen einer Dickenschwingung zugeordnet werden. »4 und »5 zeigen die Ergebnisse der experimentellen Modalanalyse für einen fein- und einen großgelochten Hochlochziegel.

Dabei treten bei dem großgelochten Hochlochziegel die Einzelsteinschwingungen bereits ab 635 Hz auf, bei dem feingelochten Hochlochziegel erst ab 920 Hz. Betrachtet man die in »2 dargestellten Verläufe des Schalldämm-Maßes der beiden Hochlochziegel, weist der Verlauf des feingelochten Hochlochziegels keine deutliche Änderung im Verlauf des Schalldämm-Maßes auf. Jedoch erkennt man im mittleren Frequenzbereich einen deutlich flacheren Verlauf des Schalldämm-Maßes. Dagegen ist bei dem Großkammerziegel eine starke Änderung im Verlauf des Schalldämm-Maßes zu erkennen, sowohl bei ca. 1200 Hz und insbesondere bei ca. 1 600 Hz. Diese Änderungen in der Schalldämmung stimmen mit den in der experimentellen Modalanalyse ermittelten Dickenschwingungen bei 1 337 Hz und bei 1 635 Hz überein. Die Messung mit der experimentellen Modalanalyse ist ein gutes Werkzeug zur Untersuchung von Einzelsteinschwingungen. Das Verfahren ist jedoch zeitaufwendig und kann nur an bereits produzierten Hochlochziegeln angewendet werden. Es ist interessant, die Ergebnisse zwischen der experimentellen und der numerischen Modalanalyse gegenüberzustellen, vor allem im Hinblick auf weiterführende Parameterstudien sowie Optimierungen der Lochgeometrien von Hochlochziegeln.

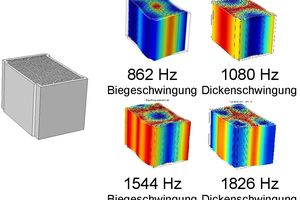
Für die numerische Modalanalyse müssen die Rohdichte, der dynamische Elastizitätsmodul und die Querkontraktionszahl des Hochlochziegels bestimmt werden. Dabei wurde der dynamische Elastizitätsmodul mit der Durchschallung mittels Ultraschall in x-, y- und z-Richtung bestimmt. In »6 und »7 sind die numerisch ermittelten Eigenfrequenzen mit den dazugehörigen Schwingformen für den groß- und feingelochten Hochlochziegel dargestellt. Die Ergebnisse der numerisch und experimentell ermittelten Eigenfrequenzen zeigen eine gute Übereinstimmung. Es kann nicht erwartet werden, dass die numerische und die experimentelle Modalanalyse exakt auf eine Frequenz genau übereinstimmen. Sowohl bei den experimentellen als auch bei den numerischen Berechnungen sind Ergebnisstreuungen zu erwarten. Dabei können unterschiedliche Materialparameter, Randbedingungen oder auch einzelne kleine Risse in dem Scherbenmaterial zu voneinander abweichenden Messergebnissen führen. Dazu werden die Eigenfrequenzen und die jeweiligen Schwingungsformen aus vielen einzelnen Übertragungsfunktionen mithilfe des Superpositionsprinzipes zu einer Übertragungsfunktion zusammengesetzt. Dies und viele weitere Faktoren führen zu einer Ergebnisstreuung bei dieser Untersuchung. Jedoch ist es gar nicht notwendig, die Eigenfrequenzen so genau zu bestimmen.

4 Parameterstudie

Durch die gute Übereinstimmung zwischen experimentell und numerisch ermittelten Eigenfrequenzen der untersuchten Hochlochziegel wurden die numerischen Ziegelmodelle für Parameterstudien herangezogen. Es wurde untersucht, welche Parameter den größten Einfluss auf die Eigenschwingungen der Hochlochziegel haben, um daraus anschließend Optimierungsmöglichkeiten für den Hochlochziegel abzuleiten.

4.1 Einfluss der Ziegeldicke auf die Eigenschwingungen

Als erster Parameter wurde der Einfluss der Hochlochziegeldicke auf die Eigenschwingungen und anschließend auf die Schalldämmung der gesamten Wand untersucht. Theoretisch ist eine Verbesserung der Schalldämmung einer gesamten Wand bei der Verwendung eines dickeren Ziegels aufgrund der zusätzlichen flächenbezogenen Masse zu erwarten.

Untersuchungen (»8) zeigen, dass die numerisch ermittelten Eigenfrequenzen des Hochlochziegels mit einer Dicke von 42,5 cm geringer im Vergleich zu dem 36,5 dicken cm Ziegel ausfallen. Dies kann auch im gemessenen Schalldämm-Maß einer gesamten Wand aus Hochlochziegeln beobachtet werden. Es ist zu erkennen, dass die Änderung in der Schalldämmung deutlicher ausgeprägt ist und sich in Richtung der tiefen Frequenzen verschiebt. Obwohl sich die flächenbezogene Masse der Wand durch die dickeren Hochlochziegel erhöht, führt dies nicht zu einer Verbesserung des bewerteten Schalldämm-Maßes einer gesamten Wand.

Analog zu der Untersuchung aus »8, zeigt der großgelochte Hochlochziegel (»9) ein identisches Verhalten. Jedoch erkennt man in dem Verlauf des Schalldämm-Maßes, obwohl die Eigenfrequenzen der Hochlochziegel abnehmen, eine Verbesserung durch das Hinzukommen der flächenbezogenen Masse. Eine Ausnahme ist dabei der 49 cm dicke Hochlochziegel. Obwohl dieser eine höhere Masse aufweist, liegt das Schalldämm-Maß unterhalb dessen des 42,5 cm dicken Hochlochziegels. Vergleicht man die Dickenschwingungen der Hochlochziegel mit den Einbrüchen in dem Verlauf des Schalldämm-Maßes der gesamten Wand, so stimmen diese, wie in der Untersuchung zuvor, mit den Eigenfrequenzen überein.

4.2 Einfluss der Material-parameter auf die Eigenschwingungen

Im nächsten Schritt wurde der Einfluss der Materialparameter auf die Eigenschwingungen des großgelochten Hochlochziegels untersucht.

»10 veranschaulicht die numerisch berechneten Eigenfrequenzen in Abhängigkeit der unterschiedlichen Scherbenrohdichte und des dynamischen Elastizitätsmoduls. Hierbei ist zu erkennen, dass die Erhöhung bzw. Verringerung des Elastizitätsmoduls und der Scherbenrohdichte keine signifikante Veränderung auf die Eigenfrequenzen des Hochlochziegels haben.

4.3 Einfluss der Lochgeometrie auf die Eigenschwingungen

Dagegen zeigen die Ergebnisse in »11 bei einer Veränderung der Lochgeometrie einen starken Einfluss auf die Eigenfrequenzen des Hochlochziegels.

Bei dieser Untersuchung wurde ein Hochlochziegel ohne sowie mit einem und mit zwei Querstegen als auch mit diagonal verlaufenden Stegen modelliert. Die Eigenfrequenzen des Hochlochziegels ohne Querstege haben, im Vergleich zu den Hochlochziegeln mit Querstegen, die tiefsten Eigenfrequenzen. Hierbei kann die Oberfläche des Hochlochziegels komplett frei schwingen und somit die Schalldämmung der gesamten Wand verschlechtern. Durch das Hinzufügen von Querstegen wird dieses Schwingverhalten vermindert, wodurch die Eigenfrequenzen in einen höheren Frequenzbereich verschoben werden. Es ist erkennbar, dass der Hochlochziegel mit zwei Querstegen im Vergleich zu den anderen untersuchten Modellen deutlich höhere Eigenfrequenzen aufweist. Interessant ist die Untersuchung des Hochlochziegels mit den diagonal verlaufenden Stegen. Die Auskreuzung führt dazu, dass die Eigenfrequenzen der Biegeschwingungen im Vergleich zu dem Ziegel mit einem Quersteg steigen und die Eigenfrequenzen der Dickenschwingungen sinken.

5 Zusammenfassung und Ausblick

Zunächst wurde beispielhaft das frequenzabhängige Schwingverhalten einer Wand aus Hochlochziegeln gezeigt. Dabei schwingen Wände aus Hochlochziegeln im tiefen Frequenzbereich wie homogene Platten. Ab dem mittleren Frequenzbereich zeigen sich einzelne Schwingungen der Hochlochziegel, die als Biege- und Dickenschwingungen bezeichnet werden.

Durch eine realitätsnahe Modellierung der Ziegelgeometrien sowie der Eigenschaften des Scherbenmaterials zeigte sich eine gute Übereinstimmung der ermittelten modalen Parameter aus experimentellen sowie numerischen Modalanalysen. Darauf aufbauend wurde eine Parameterstudie durchgeführt, um die bedeutendsten Einflussgrößen auf Einzelsteinschwingungen von Hochlochziegeln im Hinblick auf weiterführende Optimierungen der Ziegelgeometrien zu identifizieren. Hierbei resultierten aus einer zu großen Wandstärke (> 42,5 cm) Auswirkungen auf die Lage der Einzelsteinschwingungen. Dagegen zeigten Variationen der Scherbenrohdichte sowie des dynamischen Elastizitätsmoduls keine signifikanten Auswirkungen auf die Einzelsteinschwingungen.

Der größte Einfluss zeigte sich bei Veränderungen der Ziegelgeometrien, die unter anderem aus dem Integrieren von zusätzlichen Quer- sowie Diagonalstegen bestanden. Mit zunehmendem Aussteifungsgrad in Querrichtung des Ziegels verschieben sich die Einzelsteinschwingungen in höhere Frequenzbereiche. Somit stellt die Ziegelgeometrie neben den Materialeigenschaften die bedeutendste Stellschraube im Hinblick auf Optimierungen der Hochlochziegel dar.

Aus diesem Grund werden in nachfolgenden Untersuchungen weitere verschiedene Ziegelgeometrien im Hinblick auf ihr Einzelsteinschwingverhalten analysiert. Dabei werden unterschiedliche Hochlochziegeltypen ausgewählt, die die in den letzten Jahren seitens der Ziegelindustrie durch Weiterentwicklungen der Steggeometrien stetig vorgenommen Verbesserungen der Schalldämmung repräsentieren.

So soll als übergeordnetes Ziel mithilfe der messtechnischen sowie numerischen Modalanalysen versucht werden, die bereits hohen Schalldämm-Maße von Wänden aus Hochlochziegeln weiter zu optimieren. Durch eine weitere Optimierung im Hinblick auf das Schalldämm-Maß können Wände aus Hochlochziegeln weitere Anwendungen in Bereichen mit erhöhten Anforderungen an den Schallschutz von Außenbauteilen finden.